深度学习归一化方法-Batch Normalization-鲸之声

一、前言

现在几乎所有的卷积神经网络都几乎使用了批量归一化的操作
批量归一化是一种流行和有效的技术，它可以持续加速深层网络的收敛速度

二、背景

为什么需要对数据做批量归一化？
答：因为在输入数据的特征通常具有不同的量纲、取值范围，使得不同特征的尺度（scale）差异很大。不同机器学习模型对数据特征尺度的敏感程度不同。如果一个机器学习算法在数据特征缩放前后不影响其学习和预测，则称该算法具有尺度不变性（scale invariance）。理论上神经网络具有尺度不变性，但是输入特征的不同尺度会增加训练的困难，困难表现如下：

参数初始化困难
当使用具有饱和区的激活函数 $a=f(WX)$ 时，若特征 $X$ 的尺度不同，对参数 $W$ 的初始化不合适容易使激活函数陷入饱和区，产生vanishing gradient现象。
梯度下降方法效率不高
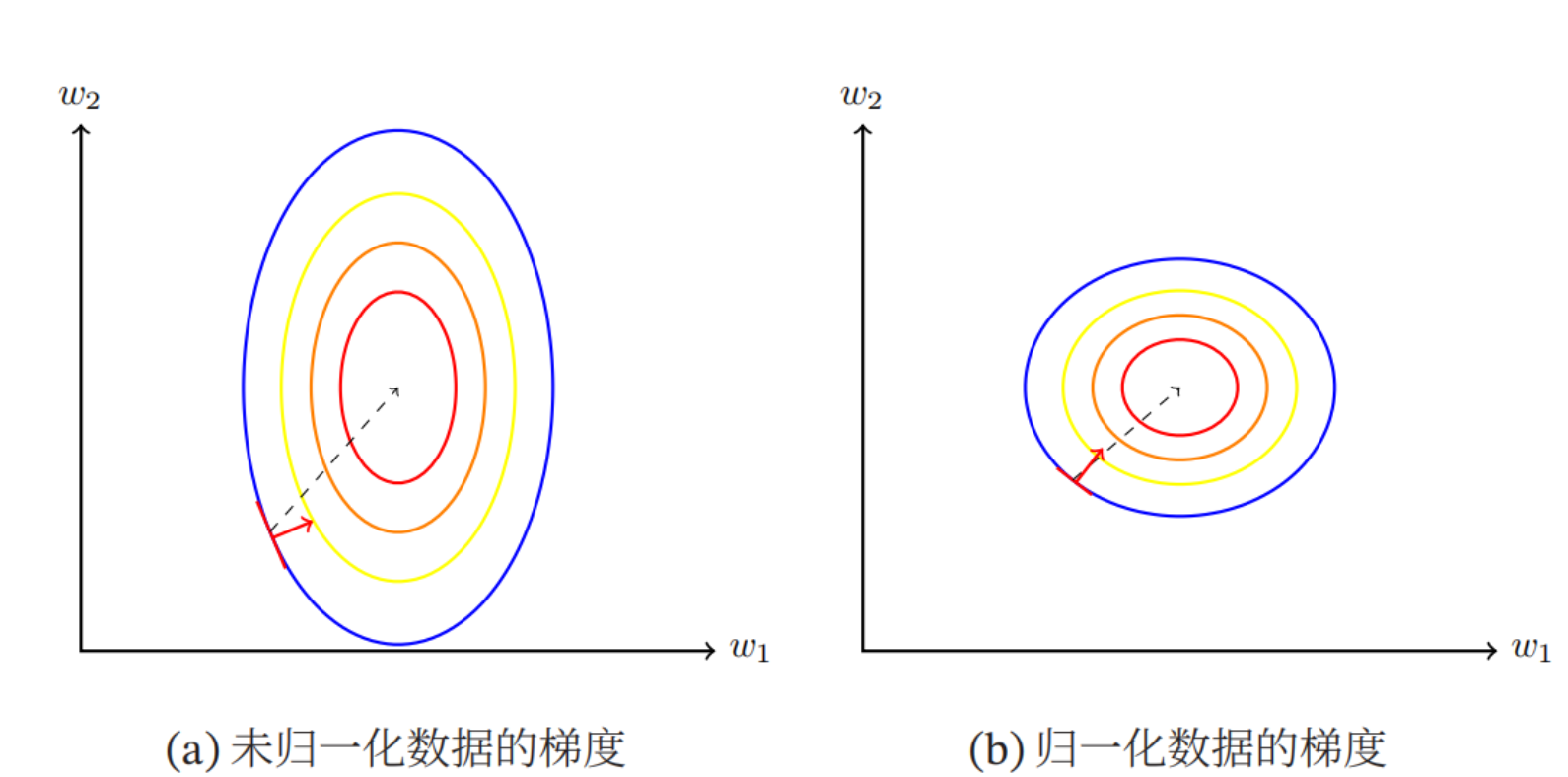
如下图所示，左图是数据特征尺度不同的损失函数等高线，右图是数据特征尺度相同的损失函数等高线。由图可以看出，前者计算得到的梯度方向并不是最优的方向，需要迭代很多次才能收敛；后者的梯度方向近似于最优方向，大大提高了训练效率。
以上两问题详细总结

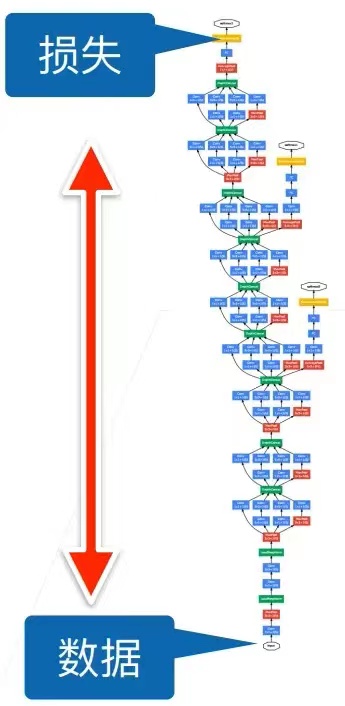
当神经网络比较深时，数据在下面，损失函数在上面。正向传播的时候，数据是一步一步往上传递，而反向传播的时候数据是从上往下传递的，这时候就会出现问题：梯度在上面的时候比较大，越往下面就越容易变得很小(根据链式求导法则，因为是n个很小的数进行相乘，越到后面结果就越小，也就是越靠近数据，层的梯度越小)。上面的梯度比较大，每次更新的时候上面的层就会不断更新；但是下面层因为梯度比较小，所以对权重地更新就比较少，这样就会导致上面层收敛比较快，而下面的收敛比较慢，这样就会导致底层靠近数据的内容(网络所抽取的网络底层的特征：简单的局部边缘、纹理等信息)变化比较慢，上层靠近损失的内容(高层语义信息)收敛比较快，所以每一次底层发生变化，所有层都在跟着变化(底层信息发生变化就会导致上层的权重白学了)，这就会导致模型的收敛速度比较慢。
因此提出了假设：能不能在改变底部信息的时候，避免顶部不断的重新训练？(这也是批量归一化所考虑的问题)

三、解决

为什么会变？ 是因为在每一层通过学习得到的输出中，方差和均值都不相同
所以假设将分布固定，假设每一层的输出、梯度都符合某一分布，相对来说就是比较稳定的(具体分布是什么样子可以商量，但是每层都符合统一分布的大环境是不能变的)
批量归一化： 将不同层的不同位置的小批量(min-batch)输出的均值和方差固定，均值和方差的计算如下：

$\mu_{B} = \frac{1}{|B|}\sum_{i\in B}x_i$

$\sigma_{B}^2 = \frac{1}{|B|}\sum_{i\in B}(x_i-\mu_B)^2+\epsilon$

B :batchsize小批量
$\epsilon$ : 方差的估计值中有一个小的常量 $\epsilon > 0$ ，作用是确保在做归一化时除数永远不等于零
在深度学习中，优化中的各种噪声源通常会导致更快的训练和较少的过拟合，这种变化似乎是正则化的一种形式，可以代替其他正则方式如dropout等。

在此基础上做出额外调整如下所示：

$x_{i+1}=\gamma \frac{x_i-\mu_B}{\sigma_B}+\beta$

给定一个来自小批量的输入 $x_i$ ，批量归一化对里面的每一个样本减去均值除以标准差，再乘以 $\gamma$ ，最后再加上 $\beta$
上式中的 $\mu_B$ 和\sigam_B是从数据中计算所得的
拉伸参数(scale) $\gamma$ 和偏移参数(shift) $\beta$ 是通过网络学习所得的参数，是批量归一化之后学出来的，作用是假设分布在某一均值方差下不适用，就可以通过学习一个新的均值和方法，使得神经网络输出的分布更好(在训练过程中，中间层的变化幅度不能过于剧烈，应用批量归一化可以将每一层主动居中，并对 $\beta$ 和 $\gamma$ 进行限制从而将他们重新调整为给定的均值和大小，避免变化过于激烈)

四、适用场合

BN适用于mini batch比较大、数据分布比较接近的场合。在进行训练之前，要做好充分的shuffle；
BN在运行过程中需要计算每个mini batch的统计量，因此不适用于动态的网络结构和RNN网络，也不适合Online Learning（batchsize = 1）。对于RNN和LSTM，我们通常采用(Layer Normalizaiton)，transformer也是采用LN归一化。