原文地址：论文地址

摘要：

时间序列中的统计属性经常发生变化，即数据分布随时间而变化。这种时间分布变化是阻碍准确时间序列预测的主要挑战之一。为了解决这个问题，我们提出了一种简单但有效的归一化方法，称为可逆实例归一化（RevIN）。具体来说，RevIN 由两个不同的步骤组成，归一化和非归一化。前者对输入进行归一化以根据均值和方差来固定其分布，而后者将输出返回到原始分布。此外，RevIN 与模型无关，通常适用于各种时间序列预测模型，预测性能有显着提高。如图 1 所示，RevIN 有效地增强了基线的性能。我们广泛的实验结果验证了对各种现实世界数据集的普遍适用性和性能改进。

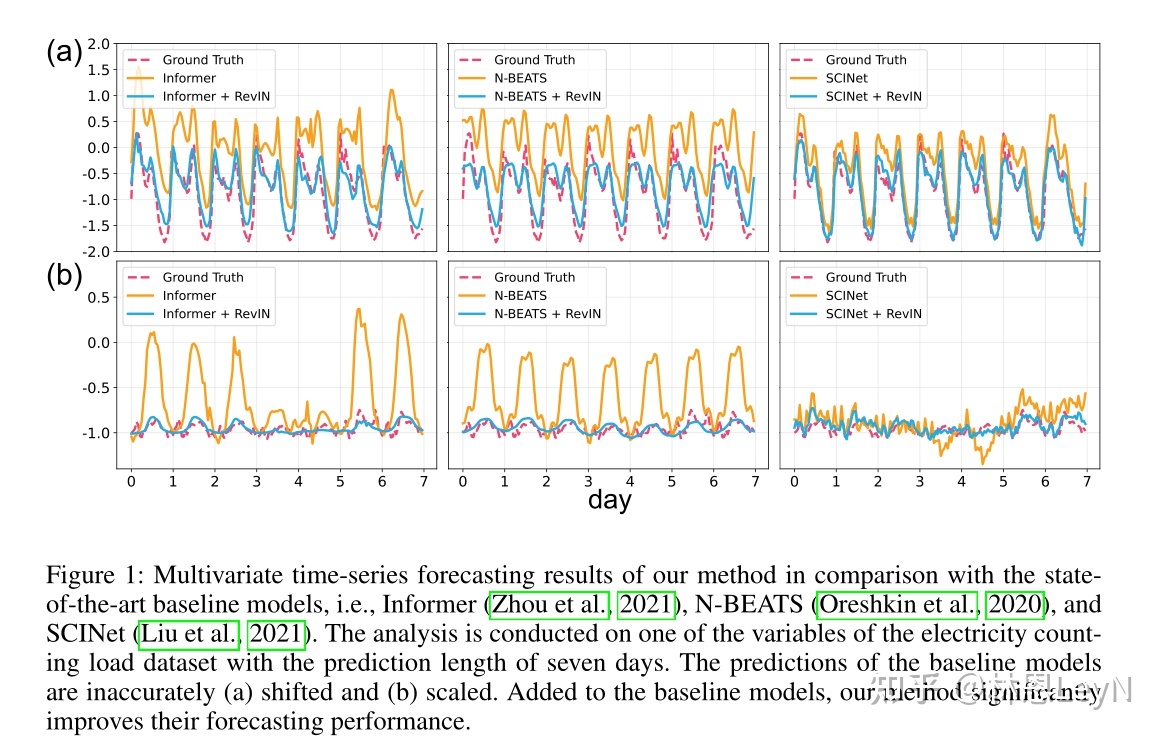
根据原作者给出的图，发现RevIN效果还是比较明显的。

Introduction

文章中认为，时序预测模型具有和其它DNN一样的性质，即对于数据输入的分布敏感。几乎所有的DNN，都是在尝试从某个数据分布中找出与之对应的值或分布，因此BN，LN这种归一化层能够让训练效果变得更好。

时序中输入分布问题在于，每一个时间戳的输入，都和上下文有关系，但是又可以看作和上下文的分布都不同，文章中采用偏移的说法。目前的Informer，N-Beats等都没有做这方面的工作，因此文章在研究后提出了RevIN：可逆实例归一化，用来在时序数据上平稳输入的分布。

Proposed Method

首先设置一些变量，后面用：

• $T_X$: 输入数据的滑动窗口大小
• $N$: 序列数量
• $K$: 变量数
• $T_y$: 预测长度
  

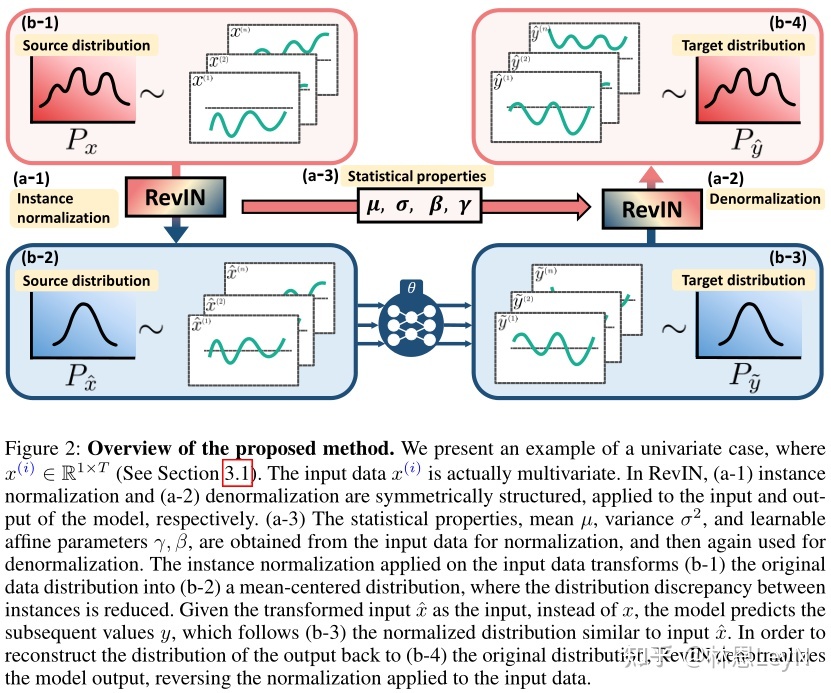
上图描述了一个基本的work flow：输入一个向量$x$，即它实际上可以看作一个多变量，每一个维度可以看作一个单变量。$x$通过RevIN，将b-1的分布转换到b-2，可以看到它的均值发生了改变，每一个单变量都针对均值做了归一化，这样原始分布中不同单变量之间的分布差异被人为的减少。将变换分布后的$\hat{x}$当作输入给网络，输出$\tilde{y}$，这些$\tilde{y}$具有b-3的分布，但也许不符合真实的分布。所以a-1的RevIN中间有一些参数，其中代表均值和方差就不提了，$\beta$是进行归一化的参数，$\gamma$是进行仿射变换的可学习参数。通过这些参数，b-3通过RevIN做一次reversing，回归近似真实的分布b-4。

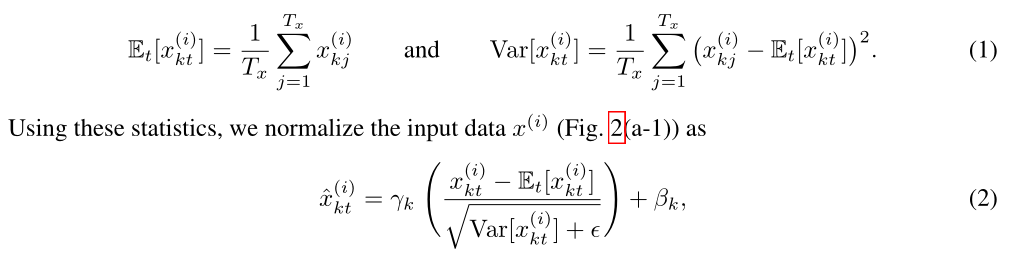
其中均值和方差的计算（1）已给出。而具体的归一化公式（2）也给出，减均值除标准差后乘$\gamma$加上$\beta$。减去均值除标准差就是典型的变成高斯分布，$\gamma$个人理解是决定了高斯峰值，$\beta$决定了偏移方向。这种归一化操作其实并不少见，上一篇博客BN归一化操作也是如此。

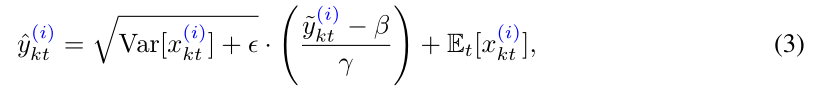
通过反转归一化，获得与输入同分布的预测值。这里的操作就是对归一化的操作取逆函数。

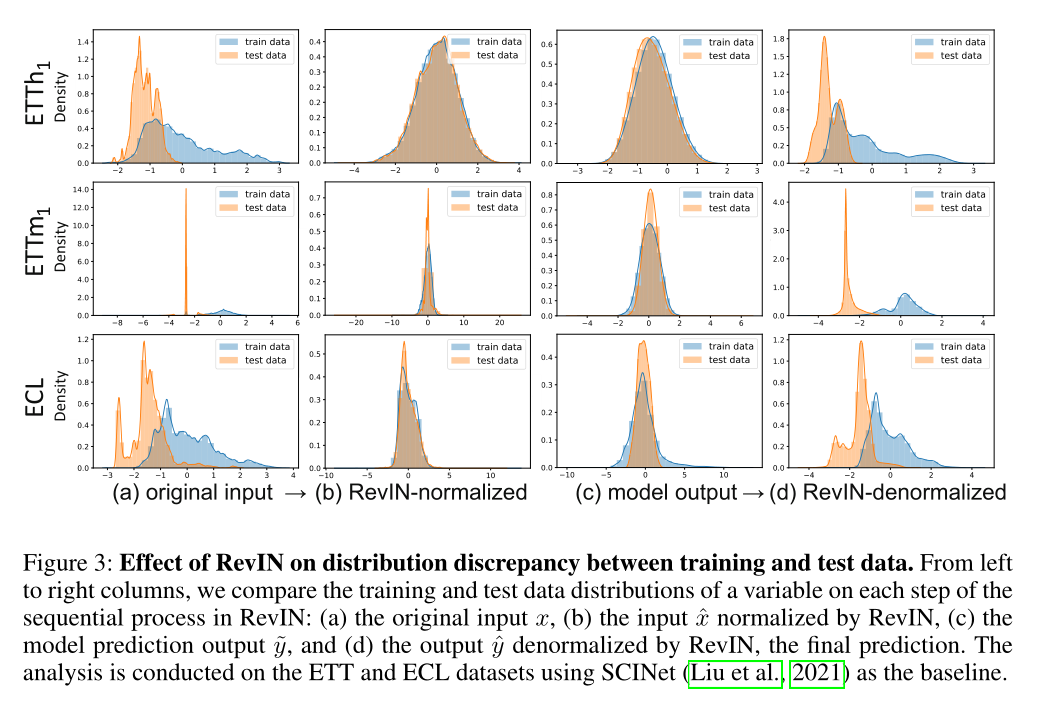
上图清楚展示了整个work flow中数据的分布变化。可以看到在分布不算太尖锐时，RevIN的归一化效果是还不错的，逆归一化时，大致的趋势相同，但是小范围的波动误差仍然广泛存在。而对于尖锐的分布，逆掉以后可以发现输出分布变平稳了，很难说这是不是好的现象。因为其与原始分布的误差已经比较明显的体现，但是在未知数据集中这种更为平稳的输出分布可能会有更好的泛化性能。

论文里提到这种过网络之前先过RevIN的结构相比传统的BN使用，更像是Encoder-Decoder，将RevIN解读维编码器/解码器也许会更好。这种层的作用并不是直接解决层间更新参数分布的偏移问题，而是有点像传统机器学习中的归一化，先清洗数据，最后反回来求。

即RevIN是一种模型无关的方法。

代码

import torch
import torch.nn as nn


class RevIN(nn.Module):
    def __init__(self, num_features: int, eps=1e-5, affine=True):
        """Reversible Instance Normalization for Accurate Time-Series Forecasting
           against Distribution Shift, ICLR2021.
        Parameters
        ----------
        num_features: int, the number of features or channels.
        eps: float, a value added for numerical stability, default 1e-5.
        affine: bool, if True(default), RevIN has learnable affine parameters.
        """
        super().__init__()
        self.num_features = num_features
        self.eps = eps
        self.affine = affine
        if self.affine:
            self._init_params()

    def forward(self, x, mode:str):
        if mode == 'norm':
            self._get_statistics(x)
            x = self._normalize(x)
        elif mode == 'denorm':
            x = self._denormalize(x)
        else:
            raise NotImplementedError('Only modes norm and denorm are supported.')
        return x

    def _init_params(self):
        self.affine_weight = nn.Parameter(torch.ones(self.num_features))
        self.affine_bias = nn.Parameter(torch.zeros(self.num_features))

    def _get_statistics(self, x):
        dim2reduce = tuple(range(1, x.ndim - 1))
        self.mean = torch.mean(x, dim=dim2reduce, keepdim=True).detach()
        self.stdev = torch.sqrt(torch.var(x, dim=dim2reduce, keepdim=True, unbiased=False) + self.eps).detach()

    def _normalize(self, x):
        x = x - self.mean
        x = x / self.stdev
        if self.affine:
            x = x * self.affine_weight
            x = x + self.affine_bias
        return x

    def _denormalize(self, x):
        if self.affine:
            x = x - self.affine_bias
            x = x / (self.affine_weight + self.eps*self.eps)
        x = x * self.stdev
        x = x + self.mean
        return x