一、前言

要设计卷积神经网络的结构，必须匹配层与层之间的输入与输出的尺寸，这就需要较好的计算输出尺寸。由于pytorch没有自动计算的函数，因此需要我们手动计算。

先列出卷积层和池化层的计算公式：

卷积后，池化后尺寸计算公式：
(图像尺寸-卷积核尺寸 + 2填充值)/步长+1
(图像尺寸-池化窗尺寸 + 2填充值)/步长+1

即：

卷积神将网络的计算公式为：
N=(W-F+2*P)/S+1
其中
N：输出大小
W：输入大小
F：卷积核大小
P：填充值的大小
S：步长大小

例Conv2d（后面给出实例来讲解计算方法）:

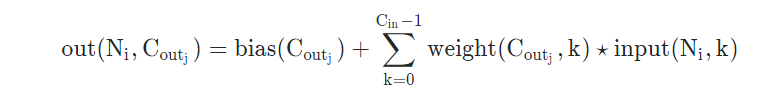
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
#卷积一层的几个参数:
in_channels=3 #表示的是输入的通道数，RGB型的通道数是3.
out_channels #表示的是输出的通道数，设定输出通道数（这个是可以根据自己的需要来设置的）
kernel_size=12 #表示卷积核的大小是12x12的，也就是上面的 F=12
stride=4 #表示的是步长为4，也就是上面的S=4
padding=2 #表示的是填充值的大小为2，也就是上面的P=2

二、实例：

cove1d：用于文本数据，只对宽度进行卷积，对高度不进行卷积 cove2d：用于图像数据，对宽度和高度都进行卷积

import torch
from torch.autograd import Variable
#torch.autograd提供了类和函数用来对任意标量函数进行求导。
import torch.nn as nn
import torch.nn.functional as F
class MNISTConvNet(nn.Module):
    def __init__(self):
        super(MNISTConvNet, self).__init__()
        '''
这是对继承自父类的属性进行初始化。而且是用父类的初始化方法来初始化继承的属性。
也就是说，子类继承了父类的所有属性和方法，父类属性自然会用父类方法来进行初始化。
        '''
#定义网络结构
        self.conv1 = nn.Conv2d(1, 10, 5)
        self.pool1 = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(10, 20, 5)
        self.pool2 = nn.MaxPool2d(2, 2)
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)
    def forward(self, input):
        x = self.pool1(F.relu(self.conv1(input)))
        x = self.pool2(F.relu(self.conv2(x)))
        x = self.fc2(self.fc1(x))
        return x

net = MNISTConvNet()
print(net)
input = Variable(torch.randn(1, 1, 28, 28))
out = net(input)
print(out.size())

我们在这个实例中抽出网络结构部分：

	self.conv1 = nn.Conv2d(1, 10, 5)
        self.pool1 = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(10, 20, 5)
        self.pool2 = nn.MaxPool2d(2, 2)
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)
    def forward(self, input):
        x = self.pool1(F.relu(self.conv1(input)))
        x = self.pool2(F.relu(self.conv2(x)))
        x = self.fc2(self.fc1(x))

网络结构为：

conv2d–maxpool2d–conv2d–maxpool2d–fullyconnect–fullyconnect

输入图片大小为：input = Variable(torch.randn(1, 1, 28, 28)) 即28*28的单通道图片，即：1 * 28 * 28

接下来，我们分层解析每一层网络的输入和输出：

1. conv2d(1,10,5)

N：输出大小
W：输入大小 28 * 28
F：卷积核大小 5 * 5
P：填充值的大小 0默认值
S：步长大小 1默认值
N=(W-F+2P)/S+1=(28-5 + 2 * 0)/1 + 1 = 24

输出为： 10 * 24 * 24
Conv2d(输入通道数, 输出通道数, kernel_size（长和宽）)，当卷积核为方形时，只写一个就可以，卷积核不是方形时，长和宽都要写，如下：

self.conv1 = nn.Conv2d(2, 4, （5，2）)

2. MaxPool2d(2, 2) MaxPool 最大池化层，池化层在卷积神经网络中的作用在于特征融合和降维。池化也是一种类似的卷积操作，只是池化层的所有参数都是超参数，是学习不到的。maxpooling有局部不变性而且可以提取显著特征的同时降低模型的参数，从而降低模型的过拟合。只提取了显著特征，而舍弃了不显著的信息，是的模型的参数减少了，从而一定程度上可以缓解过拟合的产生。

torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)

N：输出大小
W：输入大小 24 * 24
F：卷积核大小 5 * 5
P：填充值的大小 0默认值
S：步长大小 1默认值
N=(W-F+2P)/S+1=(24-2 + 2 * 0)/2 + 1 = 12

输出为： 10 * 12 * 12

3. conv2d(10,20,5)

N：输出大小
W：输入大小 12 * 12
F：卷积核大小 5 * 5
P：填充值的大小 0默认值
S：步长大小 1默认值
N=(W-F+2P)/S+1=(12-5 + 2*0)/1 + 1 = 8

输出为： 20 * 8 * 8

4. MaxPool2d(2, 2)

N：输出大小
W：输入大小 8 * 8
F：卷积核大小 5 * 5
P：填充值的大小 0默认值
S：步长大小 1默认值
N=(W-F+2P)/S+1=(8-2 + 2 * 0)/2 + 1 = 4

输出为：20 * 4 * 4

5. fully-connect Linear(320, 50)

输入：20 * 4 * 4=320
输出：50

6. fully-connect Linear(50, 10)

输入：50
输出：10

三、查询每一层的维度

可以先用容器装一下你的神经网络结构，然后再通过下面的代码进行查询

#先用容器装一下各层的网络
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

#按照图片格式生成batch_size=1,通道数为1，高宽为28像素的图片
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)

for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)

结算结果如下：

我们按照上面的公式来验证一下是否正确：

• 第一次卷积：(28-5+2*2)/1+1=28，通道数为6，因此结果为(1,6,28,28)
• 采用激活函数后不变，结果为(1,6,28,28)
• 第一次池化：(28-2+2*0)/2+1=14，因此结果为(1,6,14,14)
• 第二次卷积：(14-5+2*0)/1+1=10，通道数变为了16，因此结果为(1,16,10,10)
• 采用激活函数后不变，因此结果为(1,16,10,10)
• 第二次池化：(10-2+2*0)/2+1=5，因此结果为(1,16,5,5)
• Flatten层后为：(1,16*25)=(1,400)

Flatten可以看我另外一篇博客，默认第一维度不变，其他维度全部展开。

• 后面跟几个线性层就不用讲了