交叉熵损失函数（Cross Entropy Loss）-鲸之声

基础不牢，地动山摇，读研到现在有一年多了，发现自己对很多经常打交道的知识并不了解，仅仅是会改一改别人的代码，这使我感到非常焦虑，自此开始我的打基础之路。如果博客中有错误的地方，欢迎大家评论指出，我们互相监督，一起学习进步。

交叉熵损失函数（Cross Entropy Loss）在分类任务中出镜率很高，在代码中也很容易实现，调用一条命令就可以了，那交叉熵是什么东西呢？为什么它可以用来作为损失函数？本文将会循序渐进地解答这些问题，希望能对大家有所帮助。

1. 交叉熵（Cross Entropy）

交叉熵是信息论中的概念，想要理解交叉熵，首先需要了解一些与之相关的信息论基础。

1.1 信息量（本节内容参考《深度学习花书》和《模式识别与机器学习》）

信息量的基本想法是：一个不太可能发生的事件居然发生了，我们收到的信息要多于一个非常可能发生的事件发生。

用一个例子来理解一下，假设我们收到了以下两条消息：

A：今天早上太阳升起

B：今天早上有日食

我们认为消息A的信息量是如此之少，甚至于没有必要发送，而消息B的信息量就很丰富。利用这个例子，我们来细化一下信息量的基本想法：①非常可能发生的事件信息量要比较少，在极端情况下，确保能够发生的事件应该没有信息量；②不太可能发生的事件要具有更高的信息量。事件包含的信息量应与其发生的概率负相关。

假设 $X$ 是一个离散型随机变量，它的取值集合为 $\left { x_{1}, x_{2},\cdots , x_{n} \right }$ ，定义事件 $X=x_i$ 的信息量为：

$I(x_{i})=-\log P(X=x_{i})$

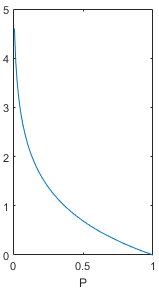
其中，log表示自然对数，底数为e（也有资料使用底数为2的对数）。公式中， $P$ 为变量 $X$ 取值为 $x_{i}$ 的概率，这个概率值应该落在0到1之间，画出上面函数在P为0-1时的取值，图像如下。在概率值 $P$ 趋向于0时，信息量趋向于正无穷，在概率值 $P$ 趋向于1时，信息量趋向于0，这个函数能够满足信息量的基本想法，可以用来描述信息量。

1.2 熵（本节内容参考《模式识别与机器学习》）

上面给出的信息量公式只能处理随机变量的取指定值时的信息量，我们可以用香农熵（简称熵）来对整个概率分布的平均信息量进行描述。具体方法为求上述信息量函数关于概率分布 $P$ 的期望，这个期望值（即熵）为：

$H(X)=-\sum_{i=1}^{n}P(X=x_{i})\log P(X=x_{i})$

让我们计算几个例题来对熵有个更深的了解。

例题①：求随机变量 $X$ 的熵，这个随机变量有8种可能的取值 $\left { x_{1}, x_{2},...,x_{8} \right }$ ，且每种取值发生的概率都是相等的，即： $P(X=x_{1})=P(X=x_{2})=...=P(X=x_{8})=\frac{1}{8}$

解：

$H(X)=-8\times \frac{1}{8}\log \frac{1}{8}=3$

例题②：还是例题①中的随机变量 $X$ ，还是8种可能的取值，但是每种取值发生的概率并不是都相等，而是如下所示： $\left { P(X=x_{1}), P(X=x_{2}),...,P(X=x_{8}) \right }=\left { \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{64}, \frac{1}{64},\frac{1}{64},\frac{1}{64}\right }$

解：

$\tiny H(X)=-\frac{1}{2}\log \frac{1}{2}-\frac{1}{4}\log \frac{1}{4}-\frac{1}{8}\log \frac{1}{8}-\frac{1}{16}\log \frac{1}{16}-\frac{1}{64}\log \frac{1}{64}-\frac{1}{64}\log \frac{1}{64}-\frac{1}{64}\log \frac{1}{64}-\frac{1}{64}\log \frac{1}{64}=2$

由例题①和例题②可以佐证《深度学习花书》中的一句结论：那些接近确定性的分布（输出几乎可以确定）具有较低的熵，那些接近均匀分布的概率分布具有较高的熵。

1.3 相对熵（KL散度）****（本节内容参考《模式识别与机器学习》）

假设随机变量 $X$ 的真实概率分布为 $P(X)$ ，而我们在处理实际问题时使用了一个近似的分布 $Q(X)$ 来进行建模。由于我们使用的是 $Q(X)$ 而不是真实的 $P(X)$ ，所以我们在具体化 $X$ 的取值时需要一些附加的信息来抵消分布不同造成的影响。我们需要的平均附加信息量可以使用相对熵，或者叫KL散度（Kullback-Leibler Divergence）来计算，KL散度可以用来衡量两个分布的差异：

$\small D_{KL}\left ( P\left | \right | Q\right )=-\sum_{i=1}^{n}P(x_{i})\log Q(x_{i})-(-\sum_{i=1}^{n}P(x_{i})\log P(x_{i}))=\sum_{i=1}^{n}P(x_{i})\log \frac{P(x_{i})}{Q(x_{i})}$

下面介绍KL散度的两个性质：

① KL散度不是一个对称量， $D_{KL}(P\left | \right |Q)\neq D_{KL}(Q\left | \right |P)$

② KL散度的值始终 $\geqslant$ 0，当且仅当 $P(X)=Q(X)$ 时等号成立

1.4 交叉熵

终于到了主角交叉熵了，其实交叉熵与刚刚介绍的KL散度关系很密切，让我们把上面的KL散度公式换一种写法：

$\tiny D_{KL}\left ( P\left | \right | Q\right )=-\sum_{i=1}^{n}P(x_{i})\log Q(x_{i})-(-\sum_{i=1}^{n}P(x_{i})\log P(x_{i}))=-H(P(X))-\sum_{i=1}^{n}P(x_{i})\log Q(x_{i})$

交叉熵 $H(P,Q)$ 就等于：

$H(P,Q)=H(P)+D_{KL}(P\left | \right |Q)=-\sum_{i=1}^{n}P(x_{i})\log Q(x_{i})$

也就是KL散度公式的右半部分（带负号）。

细心的小伙伴可能发现了，如果把 $P$ 看作随机变量的真实分布的话，KL散度左半部分的 $-H(P(X))$ 其实是一个固定值，KL散度的大小变化其实是由右半部分交叉熵来决定的，因为右半部分含有近似分布 $Q$ ，我们可以把它看作网络或模型的实时输出，把KL散度或者交叉熵看做真实标签与网络预测结果的差异，所以神经网络的目的就是通过训练使近似分布 ${\color{Red}Q }$ 逼近真实分布 ${\color{Red} P}$ 。从理论上讲，优化KL散度与优化交叉熵的效果应该是一样的。所以我认为，在深度学习中选择优化交叉熵而非KL散度的原因可能是为了减少一些计算量，交叉熵毕竟比KL散度少一项。

2. 交叉熵损失函数（Cross Entropy Loss）

刚刚说到，交叉熵是信息论中的一个概念，它与事件的概率分布密切相关，这也就是为什么神经网络在使用交叉熵损失函数时会先使用 $softmax$ 函数或者 $sigmoid$ 函数将网络的输出转换为概率值。但是据我所知，如果使用PyTorch设计网络的话，它自带的命令torch.nn.functional.cross_entropy已经将转换概率值的操作整合了进去，所以不需要额外进行转换概率值的操作。

下面从两个方面讨论交叉熵损失函数：

2.1 交叉熵损失函数在单标签分类任务中的使用（二分类任务包含在其中）

单标签任务，顾名思义，每个样本只能有一个标签，比如ImageNet图像分类任务，或者MNIST手写数字识别数据集，每张图片只能有一个固定的标签。

对单个样本，假设真实分布为 $y$ ，网络输出分布为 $\widehat{y}$ ，总的类别数为 $n$ ，则在这种情况下，交叉熵损失函数的计算方法为：

$Loss=-\sum_{i=1}^{n}y_{i}\log \widehat{y_{i}}$

用一个例子来说明，在手写数字识别任务中，如果样本是数字“5”，那么真实分布应该为：[ 0, 0, 0, 0, 0, 1, 0, 0, 0, 0 ]，
如果网络输出的分布为：[ 0.1, 0.1, 0, 0, 0, 0.7, 0, 0.1, 0, 0 ]，则 $n$ 应为10，那么计算损失函数得：

$Loss = -0\times\log 0.1-0\times \log 0.1-0\times \log0-0\times \log0-0\times \log0-1 \times \log0.7-0\times \log 0 - 0\times \log0.1-0\times \log0-0\times \log0\approx 0.3567$

如果网络输出的分布为：[ 0.2, 0.3, 0.1, 0, 0, 0.3, 0.1, 0, 0, 0 ]，那么计算损失函数得：

$Loss = -0\times\log 0.2-0\times \log 0.3-0\times \log0.1-0\times \log0-0\times \log0-1 \times \log0.3-0\times \log 0.1 - 0\times \log0-0\times \log0-0\times \log0\approx 1.2040$

上述两种情况对比，第一个分布的损失明显低于第二个分布的损失，说明第一个分布更接近于真实分布，事实也确实是这样。

对一个batch，单标签n分类任务的交叉熵损失函数的计算方法为：

$Loss=-\frac{1}{batch_size}\sum_{j=1}{batch_size}\sum_{i=1}{n}y_{ji}\log\widehat{y_{ji}}$

2.2 交叉熵损失函数在多标签分类任务中的使用

多标签分类任务，即一个样本可以有多个标签，比如一张图片中同时含有“猫”和“狗”，这张图片就同时拥有属于“猫”和“狗”的两种标签。在这种情况下，我们将 $sigmoid$ 函数作为网络最后一层的输出，把网络最后一层的每个神经元都看做任务中的一个类别，以图像识别任务为例，网络最后一层的输出应该理解为：网络认为图片中含有这一类别物体的概率。而每一类的真实标签都只有两种可能值，即“图片中含有这一类物体”和“图片中不含有这一类物体”，这是一个二项分布。综上所述，对多分类任务中的每一类单独分析的话，真实分布 ${\color{Red} P}$ 是一个二项分布，可能的取值为0或者1，而网络预测的分布 ${\color{Red} Q}$ 可以理解为标签是1的概率。此外，由于多标签分类任务中，每一类是相互独立的，所以网络最后一层神经元输出的概率值之和并不等于1。对多标签分类任务中的一类任务来看，交叉熵损失函数为：

$Loss=-y\log\widehat{y}-(1-y)\log(1-\widehat{y})$
总的交叉熵为多标签分类任务中每一类的交叉熵之和。

让我们用一个例子来理解一下，如下图所示，图中有米饭和一些菜品，假设当前的多标签分类任务有三个标签：米饭、南瓜、青菜。很明显，左边这张图是没有青菜的，它的真实分布应该为：[ 1, 1, 0 ] 。

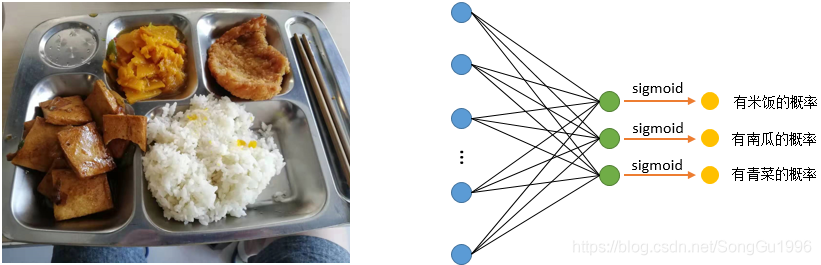
情况①：假设经过右图的网络输出的概率分布为：[ 0.8, 0.9, 0.1 ]，则我们可以对米饭、南瓜、青菜这三类都计算交叉熵损失函数，然后将它们相加就得到这一张图片样本的交叉熵损失函数值。 $Loss_{rice}=-1\times\log0.8-(1-1)\times\log(1-0.8)\approx 0.2231$
$Loss_{pumpkin}=-1\times\log0.9-(1-1)\times\log(1-0.9)\approx 0.1054$
$Loss_{greens}=-0\times\log0.1-(1-0)\times\log(1-0.1)\approx0.1054$
$\tiny Loss_{all}=Loss_{rice}+Loss_{pumpkin}+Loss_{greens}=0.2231+0.1054+0.1054=0.4339$

情况②：假设经过右图的网络输出的概率分布为：[ 0.3, 0.5, 0.7 ]，同样计算交叉熵损失函数：

$Loss_{rice}=-1\times\log0.3-(1-1)\times\log(1-0.3)\approx 1.2040$ $Loss_{pumpkin}=-1\times\log0.5-(1-1)\times\log(1-0.5)\approx 0.6931$ $Loss_{greens}=-0\times\log0.7-(1-0)\times\log(1-0.7)\approx1.2040$ $\tiny Loss_{all}=Loss_{rice}+Loss_{pumpkin}+Loss_{greens}=1.2040+0.6931+1.2040=3.1011$

由上面两种情况也可以看出，预测分布越接近真实分布，交叉熵损失越小，预测分布越远离真实分布，交叉熵损失越大。

对一个batch，多标签n分类任务的交叉熵损失函数的计算方法为：

$Loss=\frac{1}{batch_size}\sum_{j=1}{batch_size}\sum_{i=1}{n}-y_{ji}\log\widehat{y_{ji}}-(1-y_{ji})\log(1-\widehat{y_{ji}})$

参考：
一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉_史丹利复合田的博客-CSDN博客
 损失函数之交叉熵(一般用于分类问题)_ZJE_ANDY的博客-CSDN博客_交叉熵分类
 深度学习(3)损失函数-交叉熵(CrossEntropy)_theFlyer的博客-CSDN博客